- >>
- Healthy Adult Studies
- HCP Young Adult
- Project Protocols Detail
Components of the Human Connectome Project - Diffusion Tractography
MR diffusion tractography is a method for identifying anatomical connections in the living human brain. These connections form the substrate for information transfer between remote brain regions and are therefore central to our understanding of brain function.
Tractography is the only available tool for identifying and measuring these pathways non-invasively and in-vivo. By comparison with invasive techniques, tractography measurements are indirect, difficult to interpret quantitatively and error-prone. However, their non-invasive nature and ease of measurement mean that tractography studies can address scientific questions that cannot be answered by any other means. In particular, brain connections can be measured in living human subjects, and measurements can be made simultaneously across the entire brain. Hence, areal connections may be compared in humans across many cortical and sub-cortical sites. Furthermore, connections can be compared with other in-vivo measures such as functional connectivity and behavior across individuals. The Human Connectome Project is capitalizing on the key strengths of diffusion imaging. At the same time, we are investing significant effort into optimizing data acquisition strategies and tractography algorithms to maximize accuracy and minimize errors in the diffusion tractography data.
Why is diffusion useful?
Diffusion is the spread of molecules in a fluid due to constant thermal motion. The extent of this spread depends on the diffusivity of the medium. In brain white matter, tissue consists of bundles of myelinated axons. In such tissue diffusion is "hindered", i.e. it progresses more slowly than it would in water. Crucially, it is more hindered across than along such bundles. Hence, by measuring diffusion along many directions and observing that it is faster in one direction than in others, we can deduce the direction of the fiber bundles at every point in the brain.

Figure 1: Preferred diffusion directions are shown as the long axes of diffusion ellipsoids. The color is a complementary way of coding the preferred direction where red denotes left-right, green denotes back-front and blue up-down (out of the image plane). The white line shows the streamline obtained by connecting up a set of pixels based on their preferred directions and is an example of deterministic tractography.
How does tractography work?
Once we know the orientation of fibers at every point in the brain, we can join these directions up to reconstruct entire pathways and hence brain connections. In its simplest form, this consists of starting at a seed location and following the preferred direction until we reach a new measurement. We can then change to this new direction and carry on until the entire pathway is traced. This simplest technique, shown in Figure 1, is called streamline or deterministic tractography.
Small axons but big voxels.
White matter fibers in the brain have diameter on the order of 1μm, but each measurement that we can take (known as a voxel) is at the scale of approximately 1-2 mm. Hence there may be tens of thousands of axons in every voxel and they may not all be going in the same direction!! This is of course a major problem for diffusion tractography, but fortunately inter-areal connections are often organized into large bundles containing hundreds of thousands of axons that are largely coherently organized. This is the principal reason why we can examine macroscopic connectivity but not the routes of individual axons.
However, often these large fiber bundles cross each other, split or merge with one another, or fan out as they approach their destinations. These places have historically caused problems for tractography but several exciting new techniques are providing dramatically improved results. Figure 2 shows that we can estimate the orientations of 3 different fiber populations that cross each other at exactly the same place. Major technical goals of the HCP are: to compare these new techniques and select the best one; to optimize data acquisition to provide significant improvement in reconstruction accuracy; and to extend these techniques to the common situations where fiber bundles do not cross one-another, but instead spread or fan as they split or approach their destination.
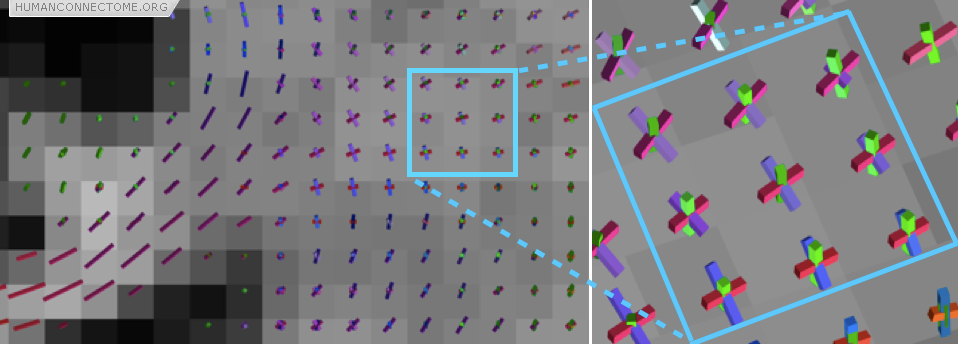
Figure 2: In this coronal section the rods show the directions of the fiber bundles that can be detected. The zoomed box shows a region where three fiber bundles are known to cross (the cortico-spinal tract, the corpus callosum and the superior longitudinal fasciculus).
Distributed connectivity and probabilistic tractography
Because our measurements come from voxels that are much larger than axons, each point in the brain does not have just one connection, but many. Furthermore, because our measurements contain errors, and our models can never be perfectly accurate, even if there were only one connection we would always be uncertain as to its exact pathway. Deterministic tractography, depicted in figure 1, can never account either for uncertainty or for distributed connectivity. Because of this, the HCP is working with probabilistic tractography. At every voxel, we estimate “most likely” fiber orientations (as in figures 1 and 2), but we also estimate a distribution representing how likely each other orientation is to lie along a fiber. Then, when we trace the connections, we trace thousands of times, each time using slightly different orientations (according to their likelihood). The set of all these different paths are then collectively a measure of the connection likelihood or probability (Figure 3). The HCP is investing significant effort in optimizing such probabilistic approaches and adapting them with new models to provide the most robust estimates of distributed connectivity for the Connectome.
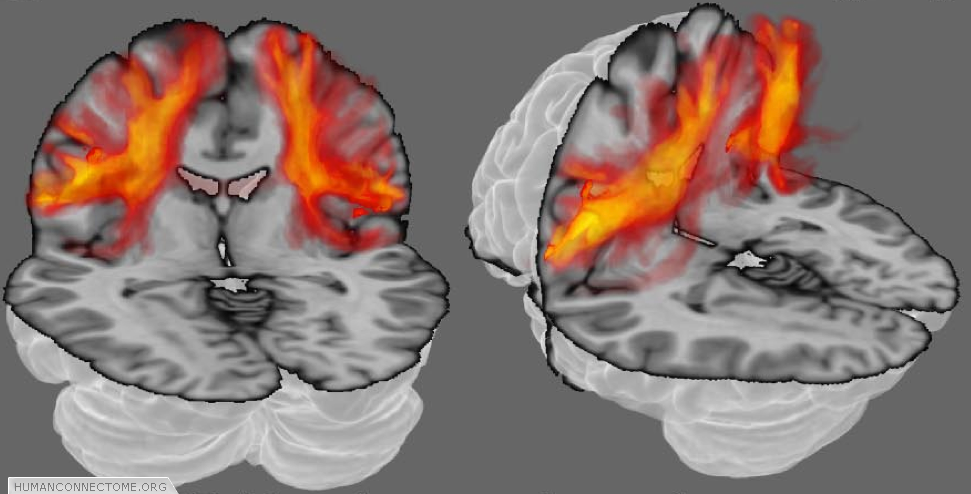
Figure 3: Probabilistic tractography. The orange clouds show color coded connectivity distributions determined by probabilistic tractography. Each voxel (point in space) is assigned a color from a hot-iron scale where black (no color in this case) means that there is zero connection probability, red-hot indicates intermediate probability and white-hot indicates a high connection probability.
How do we build a connectome matrix?
The vast majority of diffusion tractography studies to date have focused on connections of particular brain areas, performing detailed comparisons with knowledge from invasive studies in macaque monkeys, using particular connections to predict or explain particular neural responses, or relating particular connections to particular behavioral measures. In such studies, individual connections can be examined by eye and strategies can be devised and optimized for different connections. The goal of the HCP is very different. We would like to build a connection matrix summarizing the macroscopic connectivity of every brain area. This poses major challenges. We are researching strategies that work robustly across all brain areas, but are still sensitive to minor connections. We are investing significant effort into optimizing the “nodes” of the “Dense Connectome Matrix”. How many nodes do we need to capture connection differences? How should we define inter-node connectivity, given the physical distance will vary substantially between nodes? Should sub-cortical nodes and cortical nodes be treated equally? We aim to devise strategies for solving these problems that produce high test re-test reproducibility, high reproducibility across individuals. We also aim to make explicit comparisons with Dense Connectome matrices derived from resting functional connectivity and from task related activation patterns in the same individuals. These comparisons will allow us to adjudicate between strategies for building the anatomical connectome.